힙 정렬 : 힙 트리 구조 ( Heap Tree Structure)를 이용하는 정렬 방법
-> 병합 정렬 (Merge Sort) , 퀵 정렬 (Quick Sort) 만큼 빠른 정렬 알고리즘이다.
힙(Heap)이 무엇인지 알기 전에 이진 트리(Binary Tree)에 대해서 알아보자면
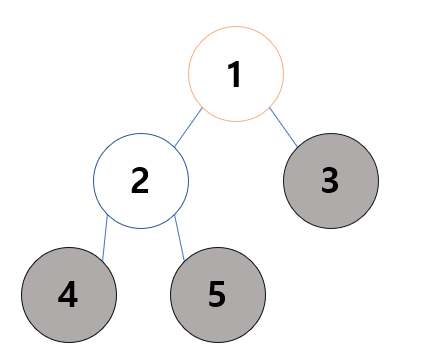
이진트리 : 컴퓨터 안에서 데이터를 표현할 때 데이터를 각 노드에 담은 뒤 노드를 두 개씩 이어 붙이는 구조 여기서 각 노드는 자식 노드가 2개 이하인 노드여야 합니다.
1 : Root(루트) 라고 하며 3, 4, 5 : Leaf(리프)하고 한다.
-> 이진트리의 종류도 많이 있는데 우선 완전 이진 트리를 알아보자면 데이터가 Root(루트) 노드 부터 시작해 자식 노드가 왼쪽 자식 노드, 오른쪽 자식 노드 순으로 차근차근 들어가는 구조의 이진 트리입니다.
즉, 이진 트리의 노드가 중간이 비어있지 않고 빽뺵히 가득 찬 구조입니다.
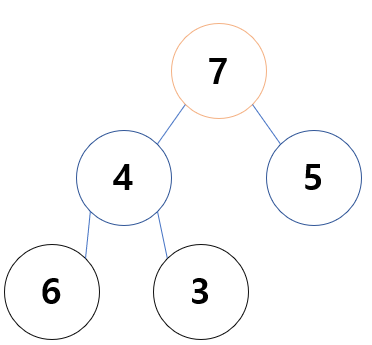
힙 : 최솟값이나 최댓값을 빠르게 찾아내기 위해 완전 이진 트리를 기반으로 하는 트리 힙에는 최소 힙과 최대 힙이 존재하는데
최대 힙 : ' 부모 노드' 가 '자식 노드' 보다 큰 힙
7 는 부모 노드 7이 자식 노드 4 5 보다 크기 때문에 최대 힙정렬이
4 5 성립된다. 하지만
4 는 부모 노드 4가 자식노드인 6 보다 작기 때문에 최대 힙 정렬이
6 8 성립되지 않는다 .
위와 같이 최대 힙정렬이 성립되지 않을 때 힙정렬을 수행하기 위해서
힙 생성 알고리즘(Heapify Algorithm)을 사용한다.
힙 생성 알고리즘
- 특정한 노드의 두 자식 중에서 더 큰 자식과 자신의 위치를 바꾸는 알고리즘
- '하나의 노드' 를 대상으로 수행하며 '하나의 노드'를 제외하고 최대 힙 정렬이 구성되 있는 상태 라고 가정을 한다.
이때 힙 생성 알고리즘의 시간 복잡도는 하나의 자식 노드로 내려갈 때마다 노드의 갯수가 2배 씩 증가한다는 점
즉 자식 노드 2개당 1개의 부모 노드이기 때문에 O(logN)입니다.
-> 3개의 데이터가 있다면 힙 생성 알고리즘을 1번만 하게 되면 최대 힙 정렬이 되기 때문에 log2N입니다.
힙 정렬은 모든 원소를 힙 생성 알고리즘을 적용시켜 최대 힙 정렬을 시키기 때문에
힙 정렬의 시간 복잡도는 N(데이터 수) * log2N(힙 생성 알고리즘 시간 복잡도)
힙 정렬의 시간 복잡도
O(N * logN)
7 6 5 8 3 5 9 1 6 를 힙 정렬로 정렬 한다면
7
6 5 --> 제시된 수를 힙 정렬 모양으로 정렬한 뒤
8 3 5 9
1 6
7
8 5 --> 6 이 최대 힙이 아니기 때문에 위치를 바꿔준다.
6 3 5 9 8 3
1 6
7
8 9 --> 5 마찬가지로 최대 힙이 아니기 때문에 위치를 바꿔준다.
6 3 5 5 5 9
1 6
9
8 7 --> 7 도 최대 힙이 아니기 때문에 바꿔주면 최대 힙 정렬이 완성된다.
6 3 5 5 8 9
1 6
6
8 7 --> 그 후 최대 힙의 Root 값 9와 제일 마지막 Leaf 값 6의 위치를 바꿔준다.
6 3 5 5
1 9
8
6 7 --> 제일 마지막 Leaf 값인 9를 제외하고 다시 최대 힙을 만들어 준다.
6 3 5 5
1 9
1
6 7 --> 그 후 다시 최대 힙의 Root 값 8와 9를 제외한 제일 마지막 Leaf 값 1의 위치를 바꿔준다.
6 3 5 5
8 9
1
3 5 --> 이 작업을 반복하여 정렬해 준다.
5 6 6 7
8 9
이렇게 9개의 원소를 가진 힙을 최대힙으로 정렬하기 위해서 힙 생성 알고리즘을 하면 logN 즉 log 9 -> 4번만 연산하면 된다.
힙 정렬은 모든 원소에 힙 정렬을 적용시키기 때문에 N (데이터 수) * logN(힙 생성 알고리즘) 이 되는 것이다.
#include<stdio.h>
int num = 9;
int heap[9] = { 7, 6, 5, 8, 3, 5, 9, 1, 6 };
int count = 0; // 연산 횟수 확인
int main(void) { // 7 6 5 8 3 5 9 1 6
// 최초 최대 힙 구성
for (int i = 1; i < num; i++) {
int c = i;
do {
int root = (c - 1) / 2; // c : 1 root : 0,
if (heap[root] < heap[c]) { // c : 2 root : 0,
int temp = heap[root]; // c : 3 root : 1,
heap[root] = heap[c]; // c : 4 root : 1
heap[c] = temp;
}
count++;
c = root;
} while (c != 0);
}
// 크기를 줄여가며 반복적으로 힙을 구성
for (int i = num - 1; i >= 0; i--) { // 1번 Leaf으로 이동하면 다신 그 위치값을 변경 할 필요가 없기 때문에 i--
int temp = heap[0]; // 0번째( 즉 Root)을 Leaf로 이동
heap[0] = heap[i];
heap[i] = temp;
int root = 0;
int c;
do { // 다시 최대 힙 정렬
c = 2 * root + 1;
printf("%d %d \n", root, c);
// 자식 중에 더 큰 값을 찾기
if (c < i - 1 && heap[c] < heap[c + 1]) { // c < i -1 를 하는 이유는
c++; // c++ 이 i가 될 경우 자리를 바꾼 최댓값이기 때문
}
// Root 보다 자식이 더 크면 변경
if (c < i && heap[root] < heap[c]) { // 값의 변동은 더 큰 값 쪽에서만 변동이 일어나기 때문에
int temp = heap[root]; // 해당 값의 자식 노드들만 힙 생성 알고리즘을 사용해주면 된다.
heap[root] = heap[c];
heap[c] = temp;
}
count++;
root = c;
} while (c < i);
}
for (int i = 0; i < num; i++) {
printf("%d ", heap[i]);
}
}
위 예제에서도 연산을 할 때마다 count 변수에 값을 +1해주었는데 결과로 count의 값은 36
즉 9 * log9 -> 9 * 4 = 36이 되었다.
힙 정렬은 병합 정렬과는 다르게 별도의 추가적인 배열이 필요하지 않다는 점에서 메모리 측면에서 몹시 효율적이다.
또 항상 O(N * log N)을 보장할 수 있다는 점에서도 몹시 강력한 정렬 알고리즘입니다.
이론적으로는 퀵 정렬, 병합 정렬보다 우위에 있다고 할 수 있지만 단순 속도만 비교하면 퀵 정렬이 평균적으로
더욱 빠르기 때문에 힙 정렬은 일반적으로는 많이 사용되지 않습니다.
'알고리즘 > 풀이 힌트' 카테고리의 다른 글
| [알고리즘] Stack ( 스택 ) (3) | 2022.02.11 |
|---|---|
| [알고리즘] 계수 정렬 (0) | 2022.02.10 |
| [알고리즘] C++ STL sort() 함수_Vector/Pair (2) | 2022.02.10 |
| [알고리즘] C++ STL sort() 함수_class (0) | 2022.02.10 |
| [알고리즘] 퀵 정렬_구현 (0) | 2022.02.09 |
