크루스칼 알고리즘 : 가장 적은 비용으로 모든 노드를 연결하기 위해 사용되는 알고리즘
최소 비용 신장 트리를 만들기 위한 대표적인 알고리즘입니다.
※ 신장 트리 : 그래프 내의 모든 노드를 포함하는 트리
노드 = 정점 = 도시 : 그래프에서 동그라미에 해당하는 부분
간선 = 거리 = 비용 : 그래프에서 선에 해당하는 부분
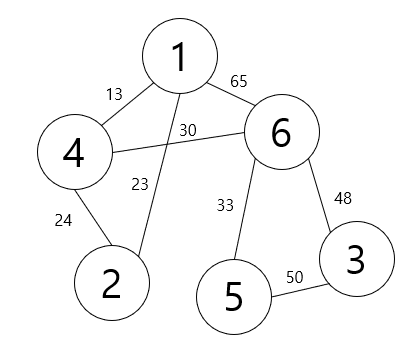
위 그래프를 살펴보았을 때 6개의 노드와 8개의 간선이 있습니다. 해당 그래프를 크루스 칼 알고리즘을
적용시켜 본다면 아래와 같습니다.
잠시 그래프에서 모든 노드를 연결하기 위해 최소한으로 필요한 간선의 수는
N( 노드) - 1개입니다. 즉 위 그래프는 노드가 6개 있으므로 최소 비용 신장 트리를 만들기 위해 필요한 간선의 수는 5개입니다.
일단 모든 노드를 최대한 적은 비용으로 ' 연결만 ' 시키면 되기 때문에 모든 간선 정보를 오름차순으로 정렬한 뒤
비용이 적은 간선부터 차근차근 그래프에 포함시키는 것입니다.
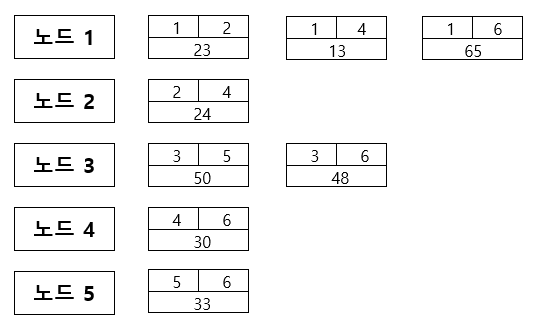
위와 같이 모든 간선들의 정보를 저장합니다. 노드 1부터 노드 7까지 연결된 모든 간선의 정보를 저장한 것입니다.
노드 6은 간선 정보가 없는데, 이미 다른 노드의 간선 정보에 포함되어 있기 때문이다.
이렇게 살펴 보니 앞서 말한 것과 같이 간선이 총 8개가 존재합니다.
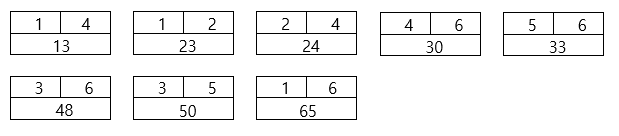
간선을 ' 거리(비용) '을 기준으로 먼저 오름차순 정렬을 수행하였습니다.
이를 토대로 알고리즘에 맞게 그래프를 연결하면 가장 적은 비용으로 모든 노드를 연결한 그래프인
' 최소 비용 신장 트리 ' 가 만들어집니다.
이제 최소 비용 신장 트리의 조건을 보자면
1. 정렬된 순서에 맞게 그래프에 포함시킵니다.
2. 포함시키기 전에는 사이클 테이블을 확인합니다.
3. 사이클을 형성하는 경우 간선에 포함하지 않습니다.
여기서 말하는 ' 사이클 ' 이란 것은 그래프가 서로 연결되어 사이클을 형성하는 경우입니다.
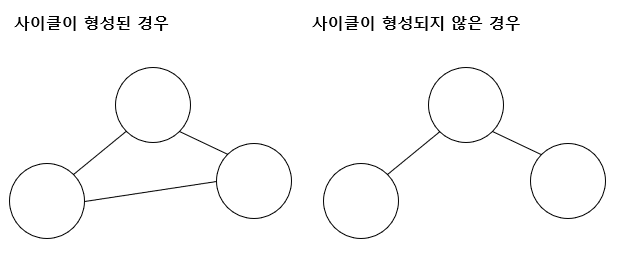
이러한 사이클이 최소 비용 신장 트리에서는 발생하면 안 됩니다.
사이클이 발생하는지 여부는 바로 앞에 배운 Union - Find 알고리즘( 바로 여기서 사용! )을 적용하면 됩니다.
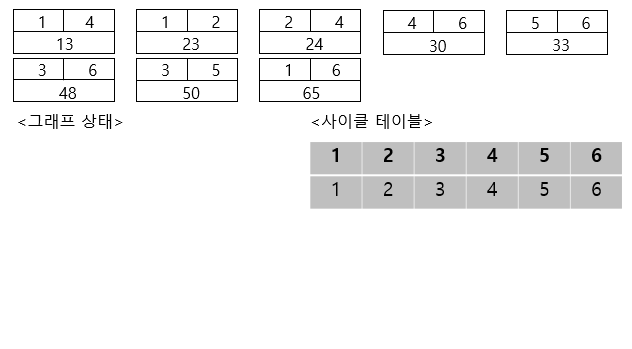
바로 시작하자면, 아래 그림은 초기 상태입니다.
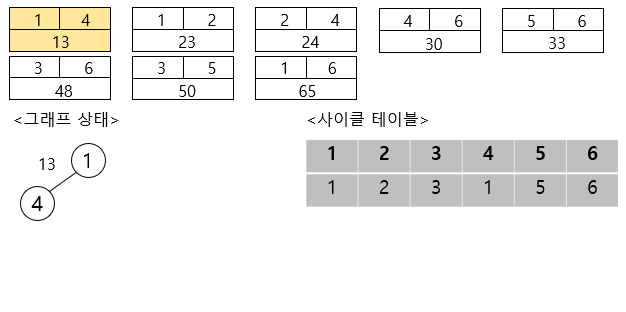
이제 첫 번째 간선을 선택하여 보면, ( 이때 사이클 테이블의 값도 동일하게 변경해줍니다.)
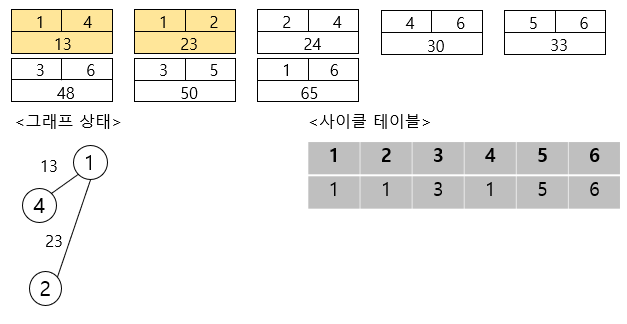
이제 두 번째 간선을 선택하여 보자면,
이 기세를 몰아 세 번째 간선을 선택하여 보자면,
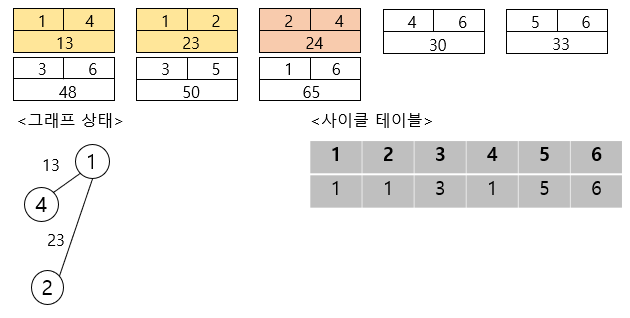
여기서 문제가 발생합니다. 노드 2와 노드 4를 연결하면 사이클이 형성되기 때문에 무시하고 넘어갑니다.
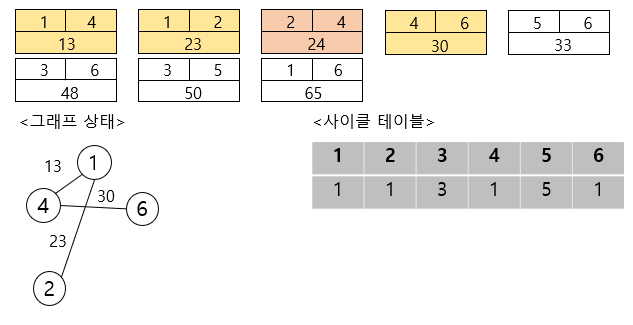
그러므로 노드 4와 노드 6을 연결하여 줍니다.
그 후 네 번째 간선을 연결하여 보자면,
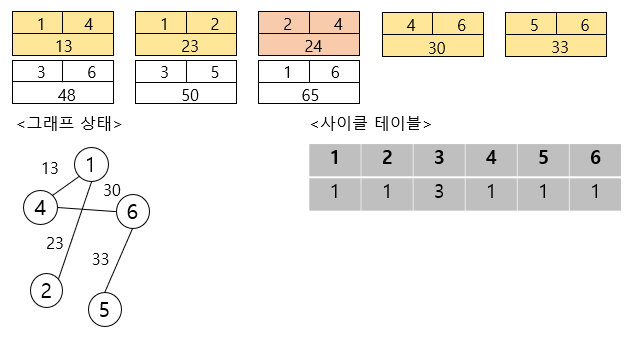
이제 다섯 번째 간선을 연결하여 보자면,
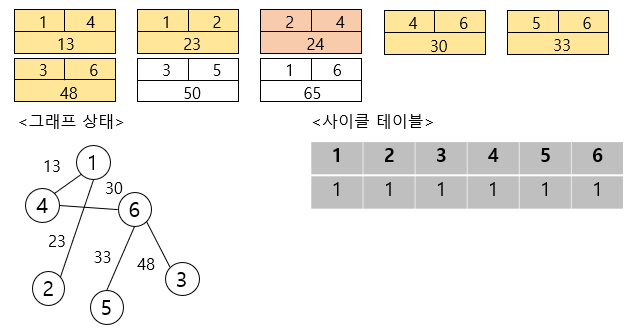
이렇게 사이클 테이블의 모든 값이 1이 되면서 최소 비용 신장 트리가 만들어진 것을 알 수 있습니다.
나머지 2개의 간선은 모두 스킵(Skip) 처리되면서 결과적으로 다음과 같이 완성됩니다.
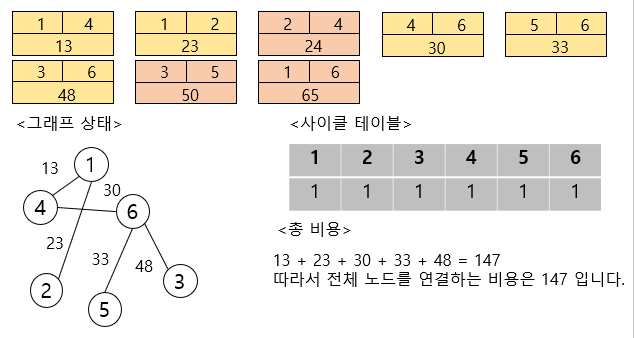
자 이제 소스 코드로 구현을 해보자면,
#include <vector>
#include <iostream> // C++ 헤더
#include <algorithm> // STL 라이브러리 -> sort() 함수가 정의되어있음
using namespace std;
// 부모 노드를 찾는 함수
int getParent(int parent[], int x) {
if (parent[x] == x) return x;
else return parent[x] = getParent(parent, parent[x]);
}
// 두 부모 노드를 합치는 함수
void unionParent(int parent[], int a, int b) {
a = getParent(parent, a);
b = getParent(parent, b);
if (a < b) {
parent[b] = a;
printf("%d\n", b);
}
else {
parent[a] = b;
printf("%d\n", a);
}
}
// 같은 부모를 가지는지 확인
int findParent(int parent[], int a, int b) {
a = getParent(parent, a);
b = getParent(parent, b);
if (a == b) return 1;
else return 0;
}
// 간선 클래스 선언
class Edge {
public :
int node[2];
int distance;
Edge(int a, int b, int distance) {
this->node[0] = a;
this->node[1] = b;
this->distance = distance;
}
bool operator<(Edge &edge) {
return this->distance < edge.distance;
}
};
int main(void) {
const int n = 6;
int m = 8;
vector<Edge> v;
v.push_back(Edge(1, 4, 13));
v.push_back(Edge(1, 2, 23));
v.push_back(Edge(1, 6, 65));
v.push_back(Edge(2, 4, 24));
v.push_back(Edge(3, 5, 50));
v.push_back(Edge(3, 6, 48));
v.push_back(Edge(4, 6, 30));
v.push_back(Edge(5, 6, 33));
// 간선의 비용을 기준(Edge 클래스의 operator)으로 오름차순 정렬
sort(v.begin(), v.end());
// 각 정점이 포함된 그래프가 어디인지 저장
int set[n];
for (int i = 0; i < n; i++) {
set[i] = i;
}
// 거리의 합을 0으로 초기화
int sum = 0;
for (int i = 0; i < v.size(); i++) {
// 동일한 부모를 가르키지 않는 경우, 즉 사이클이 발생하지 않을 때만 간선 선택
if (!findParent(set, v[i].node[0] - 1, v[i].node[1] - 1)) {
sum += v[i].distance;
unionParent(set, v[i].node[0] - 1, v[i].node[1] - 1);
}
}
printf("%d\n", sum);
}마찬가지로 자바로 구현해보자면!
import java.util.ArrayList;
import java.util.Collections;
public class Study_Kruskal_Algorithm {
public static int getParent(int[] parent, int x) {
if(parent[x] == x) return x;
else return getParent(parent,parent[x]);
}
public static void UnionParent(int[] parent,int x,int y) {
int a = getParent(parent, x);
int b = getParent(parent, y);
if(a < b) parent[b] = a;
else parent[a] = b;
}
public static boolean FindParent(int[] parent,int x, int y) {
int a = getParent(parent, x);
int b = getParent(parent, y);
if(a == b) return true;
else return false;
}
public static void main(String[] args) {
// TODO 자동 생성된 메소드 스텁
int n = 6;
int m = 8;
ArrayList<Edge> a = new ArrayList<Edge>();
a.add(new Edge(1, 2, 23));
a.add(new Edge(1, 4, 13));
a.add(new Edge(1, 6, 65));
a.add(new Edge(2, 4, 24));
a.add(new Edge(3, 5, 50));
a.add(new Edge(3, 6, 48));
a.add(new Edge(4, 6, 30));
a.add(new Edge(5, 6, 33));
Collections.sort(a);
int[] set = new int[n];
for(int i = 0; i < n; i++)
set[i] = i;
int sum = 0;
for(int i = 0;i < a.size(); i++) {
if(!FindParent(set, a.get(i).node[0]-1, a.get(i).node[1]-1)) {
sum += a.get(i).distance;
UnionParent(set, a.get(i).node[0]-1, a.get(i).node[1]-1);
}
}
System.out.println(sum);
}
}
class Edge implements Comparable<Edge>{
int[] node = new int[2];
int distance;
public Edge(int a, int b, int distance) {
this.distance = distance;
this.node[0] = a;
this.node[1] = b;
}
@Override
public int compareTo(Edge edge) {
if(this.distance > edge.distance)
return 1;
else
return -1;
}
}'알고리즘 > 풀이 힌트' 카테고리의 다른 글
| [알고리즘] 자료구조? 알고리즘? (0) | 2022.04.10 |
|---|---|
| [알고리즘] 휴리스틱 알고리즘 (1) | 2022.03.20 |
| [알고리즘] 깊이 우선 탐색 ( Depth First Search : DFS ) (4) | 2022.02.14 |
| [알고리즘] 너비 우선 탐색( Breadth First Search, BFS) (3) | 2022.02.13 |
| [알고리즘] Queue ( 큐 ) (6) | 2022.02.12 |
