문제 설명
가로 길이가 Wcm, 세로 길이가 Hcm인 직사각형 종이가 있습니다. 종이에는 가로, 세로 방향과 평행하게 격자 형태로 선이 그어져 있으며, 모든 격자칸은 1cm x 1cm 크기입니다. 이 종이를 격자 선을 따라 1cm × 1cm의 정사각형으로 잘라 사용할 예정이었는데, 누군가가 이 종이를 대각선 꼭지점 2개를 잇는 방향으로 잘라 놓았습니다. 그러므로 현재 직사각형 종이는 크기가 같은 직각삼각형 2개로 나누어진 상태입니다. 새로운 종이를 구할 수 없는 상태이기 때문에, 이 종이에서 원래 종이의 가로, 세로 방향과 평행하게 1cm × 1cm로 잘라 사용할 수 있는 만큼만 사용하기로 하였습니다.
가로의 길이 W와 세로의 길이 H가 주어질 때, 사용할 수 있는 정사각형의 개수를 구하는 solution 함수를 완성해 주세요.
제한사항
- W, H : 1억 이하의 자연수
입출력
| W | H | result |
| 8 | 12 | 80 |
입출력 예
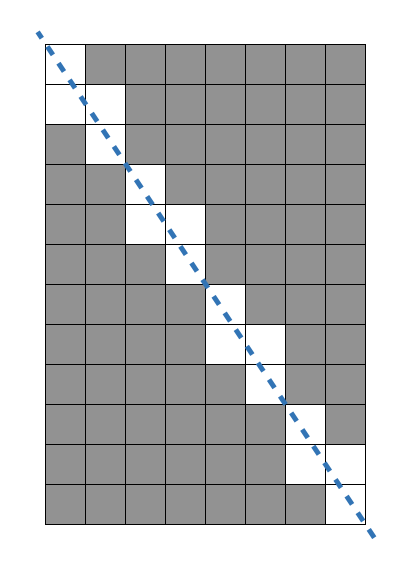
가로가 8, 세로가 12인 직사각형을 대각선 방향으로 자르면 총 16개 정사각형을 사용할 수 없게 됩니다. 원래 직사각형에서는 96개의 정사각형을 만들 수 있었으므로, 96 - 16 = 80 을 반환합니다.
나의 풀이
const w = 1;
const h = 7;
function solution(w, h) {
let num1 = w;
let num2 = h;
if (num1 < num2) {
let tmp = num1;
num1 = num2;
num2 = tmp;
}
while (num2 !== 0) {
let gcd = num1 % num2;
num1 = num2;
num2 = gcd;
}
if (num1 === 1) {
return w * h - (w + h - 1);
} else {
return w * h - (w + h - num1);
}
}
console.log(solution(w, h));대각선이 내부 격자점이 존재하지 않는다면,
잘리는 사각형이 " 가로 + 세로 - 1 " 규칙을 적용했고 대각선이 내부 격자점이 존재한다면,
잘리는 사각형이 " 가로 + 세로 - 가로 세로의 최대 공약수 " 라는 규칙을 사용해서 풀었다.
다른 사람의 풀이
function solution(w, h) {
const slope = h / w;
let result = 0;
for (let i = 1; i <= w; i++) {
result += Math.ceil(slope);
}
return h * w - result;
}
예시의 이미지를 좌우 반전하면 그래프 형식으로 나와있는 것을 확인할 수 있다.
여기서 x가 1 증가할 때마다 y는 1.5가 증가하는 것을 확인할 수 있는데, 사각형을 기준으로 했을때는
1.5개는 2개와 같다.
즉, x가 1씩 증가할때마다 사각형이 2개씩 감소된다고 보면된다.
그러므로 반복문을 통해서 w만큼 반복하고 지워지는 사각형 수를 더해주고 마지막에 빼면 결과가 나온다.
그래프를 사용하고, 올림 작업을 통해 지워지는 사각형을 만드는 방식이 대단하다....
출처: 프로그래머스 코딩 테스트 연습, https://programmers.co.kr/learn/challenges
'알고리즘' 카테고리의 다른 글
| [알고리즘] 기능 개발 (1) | 2022.05.13 |
|---|---|
| [알고리즘] 124 나라의 숫자 (1) | 2022.05.12 |
| [알고리즘] 없는 숫자 더하기 (3) | 2022.05.07 |
| [알고리즘] 크레인 인형뽑기 게임 (2) | 2022.05.06 |
| [알고리즘] 키패드 누르기 (1) | 2022.05.01 |
